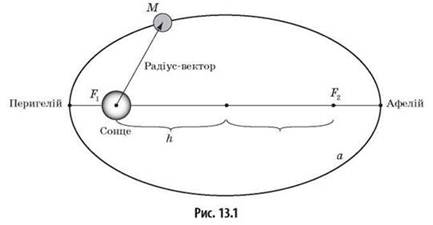
"Квадрат орбітального періоду планети пропорційний кубу півмайори осі його орбіти". Це третій закон Кеплера. Іншими словами, якщо скласти квадрат "року" кожної планети і поділити його на куб її відстані до Сонця, ви отримаєте однакове число для всіх планет.
(Інші два - «орбіта кожної планети - це еліпс із Сонцем у фокусі», а «лінія між планетою та Сонцем промітає рівні площі за рівний час».)
Коперник, Кеплер і Ньютон завдали удару двома-трьома нокаутами - тисячі років - про те, що Сонце (і планети) рухалися навколо Землі. Коперник поставив Сонце в центр, Кеплер змінив кругові рухи Коперника (і надав простий, кількісний опис фактичного руху), а Ньютон пояснив, як це все працює (сила тяжіння).
Кеплер розробив свої три закони з детальних записів спостережень за положеннями планет (відомих на той час, Меркурія, Венери, Марса, Юпітера та Сатурна) - особливо Марса - старанно складених Тіхо Браге.
Третій закон Кеплера (насправді всі три) працює не тільки для планет у нашій Сонячній системі, але і для лун усіх планет, карликових планет і астероїдів, супутників, що обходять навколо Землі і т. Д. Ну, не зовсім; якщо вторинне тіло - планета, скажімо, - має масу, яка є значною часткою первинного (Сонце, скажімо), то закон потребує невеликої зміни.
Показавши, як закони Кеплера можуть бути виведені з його універсального закону тяжіння, Ньютон об'єднав небо і землю, можливо, найбільшу революцію в науці (гаразд, революція Дарвіна може бути більшою). До Ньютона вважалося, що небо працює за правилами, зовсім іншими, ніж правила, що регулювали речі на Землі.
NASA - Уявіть Всесвіт! має чітку демонстрацію законів Кеплера, і цей PDF-файл (з кафедри математики Університету штату Тенесі Ноксвілл) дає просте виведення законів Кеплера від загального закону тяжіння Ньютона.
Статті з космічного журналу з додатковою інформацією: Закони Кеплера, Давайте вивчати закон: Кеплер буде так гордий і з днем народження Йоганнес Кеплер.
Гравітація, епізод астрономічної ролі, також обговорює третій закон Кеплера, а також де Де знаходиться Центр Всесвіту ?.